Associate Professor Helen Chick (2025)

Associate Professor Helen Chick (OEIC2025)

Associate Professor (A/P) Helen Chick is a distinguished academic and experienced practitioner who holds a PhD in Mathematics from the University of Tasmania and is a qualified secondary school Mathematics teacher in Australia. Her excellence in teaching has been recognised through several awards in Australia, including Teaching Excellence Awards and Teaching Merit Certificates. A/P Helen's research and classroom practice focus on pedagogical content knowledge, emphasising effective use of examples, statistics education, and explicit teaching models in Mathematics. She has extensive experience providing professional learning programmes for the Department of Education, Australia, working with both pre-service and in-service teachers across primary and secondary levels.

Her work on mathematical reasoning and problem-solving aligns closely with Singapore's Mathematics Problem-Solving Framework, as demonstrated through her significant contributions in developing "Explicit Teaching" modules and her Grade 6 teaching videos that translate complex pedagogical concepts into practical strategies. With her deep understanding of Mathematics pedagogy, passion for enhancing student learning, and proven track record in teacher development, A/P Helen is ideally suited to inspire and upskill Singapore's Mathematics teachers. Her expertise in explicit teaching, problem-solving, and effective classroom dialogue was invaluable in enhancing our educators' capabilities.

Overview of Collaboration between Outstanding Educator (OE), Master Teachers (MTT) and Teacher Collaborator (TC)

Overview of MLD1 and MMTL Webinars

Keynote Address at Mathematics Learning Day 1 (22 April)

Critical, Adaptive, and Inventive Thinking in the Mathematics Classroom

This keynote presentation by A/P Helen explored how Critical, Adaptive, and Inventive Thinking (CAIT) can be fostered in Mathematics education. The presentation demonstrated that developing CAIT requires deliberate teacher effort in planning, task selection, classroom culture development, and questioning. Importantly, fostering CAIT in students also requires CAIT from teachers themselves. The overarching message was that Mathematics classrooms can indeed be spaces for creative, critical thinking when teachers thoughtfully design tasks, cultivate appropriate classroom cultures, and employ strategic teaching actions.

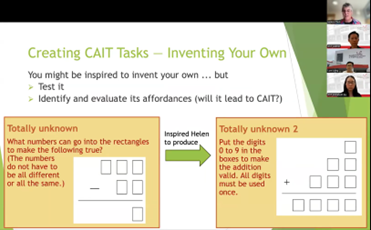
Keynote Address at Professional Learning Session 2 for MMs/TLs (29 July)

Planning for Explicit Learning in Mathematics to Deepen Connections

This presentation by A/P Helen Chick focused on planning Mathematics lessons for explicit learning. The session emphasised that planning is critical as it challenges teachers to identify what explicit learning they want for their students. Teachers may make different planning decisions, but what matters are the reasons for their choices. Thinking carefully about examples, tasks, questions, and connections can significantly impact student learning, as teaching is fundamentally about ensuring students learn.

Overview of Lesson Demonstration at Casuarina Primary School

A/P Helen collaborated with our local Teacher Collaborator, Mrs Sarah Teng (Senior Teacher/Mathematics, Casuarina Primary School), to design and enact a lesson on ‘Fraction as Part of a Whole’ for Primary 2 students.

The lesson systematically built students' understanding of unit fractions through review, exploration, and application.

Throughout each phase, consistent questioning encouraged students to identify patterns in notation, naming conventions, and the relationship between denominators and equal parts, whilst comparing fraction sizes to develop proportional reasoning.

The lesson concluded with an interactive matching activity where students identified and grouped fraction cards based on mathematical properties, effectively consolidating understanding through hands-on manipulatives and collaborative learning.

Overview of Lesson Demonstration at Changkat Changi Secondary School

A/P Helen collaborated with our local Teacher Collaborator, Ms Huang Yaling (Senior Teacher/Mathematics, Changkat Changi Secondary School), to design and enact a lesson on ‘Line Graphs’ for Secondary 1 students.

The lesson systematically developed students' understanding of line graphs through critical analysis of flawed infographics, practical construction using real-world temperature data of Singapore and Hobart, and comparative interpretation techniques.

Beginning with examination of a deliberately problematic infographic to establish graphs as tools for revealing data patterns, students progressed through structured exploration where they plotted multiple datasets on shared axes, discovering how visual representation makes patterns more apparent than tabular data when examining seasonal variation and geographical differences.

The lesson effectively integrated guided questioning about design choices, scale selection, and axis labelling, while extending learning through rainfall analysis and bar graph comparison, demonstrating how hands-on graphing activities can enhance students' ability to interpret and construct meaningful statistical representations that facilitate direct data comparison and trend analysis.

Overview of Workshops

A/P Helen conducted four workshops which explored how strategic questioning transforms Mathematics learning by developing students' CAIT capabilities. Participants examined six evidence-based question types that enhance classroom discourse and mathematical reasoning: Reasoning Questions ("How do you know?") that emphasise justification and reveal student thinking, Hypothetical Exploration ("What happens if...?") that develops key mathematical ideas and extends thinking, Example Generation ("Can you give me an example of...?") that builds students' conceptual understanding through varied examples, Conditional Reasoning ("Sometimes, always or never true?") that explores when principles apply and develops logical thinking, Fermi Questions that develop real-world problem-solving and estimation skills, and Backwards Questions ("If this is the answer, what might the question have been?") that emphasise mathematical structure and reversibility.

Through practical implementation strategies and classroom application examples, teachers gained insights into the power of purposeful questioning to help students generalise, form Mathematical abstractions, and engage in deeper mathematical reasoning within active questioning environments.

Feedback from Workshop Participants

Participants found the workshop on questioning techniques to be highly practical and immediately applicable to their classroom practice. They particularly valued the structured six question types framework, which provided ready-to-use templates with clear purposes for developing students' Critical, Adaptive and Inventive Thinking (CAIT). Using these questions strategically make students’ thinking visible and help students develop Mathematical generalisations.

There were strong interests for specific questioning strategies, especially "What if" questions for deepening conceptual understanding, Fermi questions for real-world problem-solving, and "Sometimes/always/never true" statements for promoting Mathematical communication. Teachers also appreciated backwards questioning techniques and found the "How do you know" prompts effective for encouraging student reasoning.

Contextualisation and Application by our Teacher Collaborators

Our Teacher Collaborators, Mrs Sarah Teng (ST/Mathematics, Casuarina Primary School) and Ms Huang Yaling (ST/Mathematics, Changkat Changi Secondary School) both contextualised and applied the questioning techniques they gleaned from A/P Helen in their own classrooms.

Sarah’s innovative fractions lesson at Casuarina Primary School demonstrated exemplary use of the Concrete-Pictorial-Abstract approach, where students explored halves and quarters through hands-on manipulation of square paper "brownies" before progressing to mathematical notation. Building on familiar concepts from the "Give me half" story, students discovered that equal parts can look different while maintaining the same size, developing deep conceptual understanding through active learning strategies including peer sharing, class discussions, and visual representations. The lesson effectively integrated formative assessment through continuous checking for understanding, thumbs up/down responses, and exit tickets, while employing strategic questioning techniques to elicit student thinking and build mathematical understanding through meaningful dialogue, ultimately helping students grasp the concept that fractions represent equal parts of a whole before introducing abstract symbols and terminology.

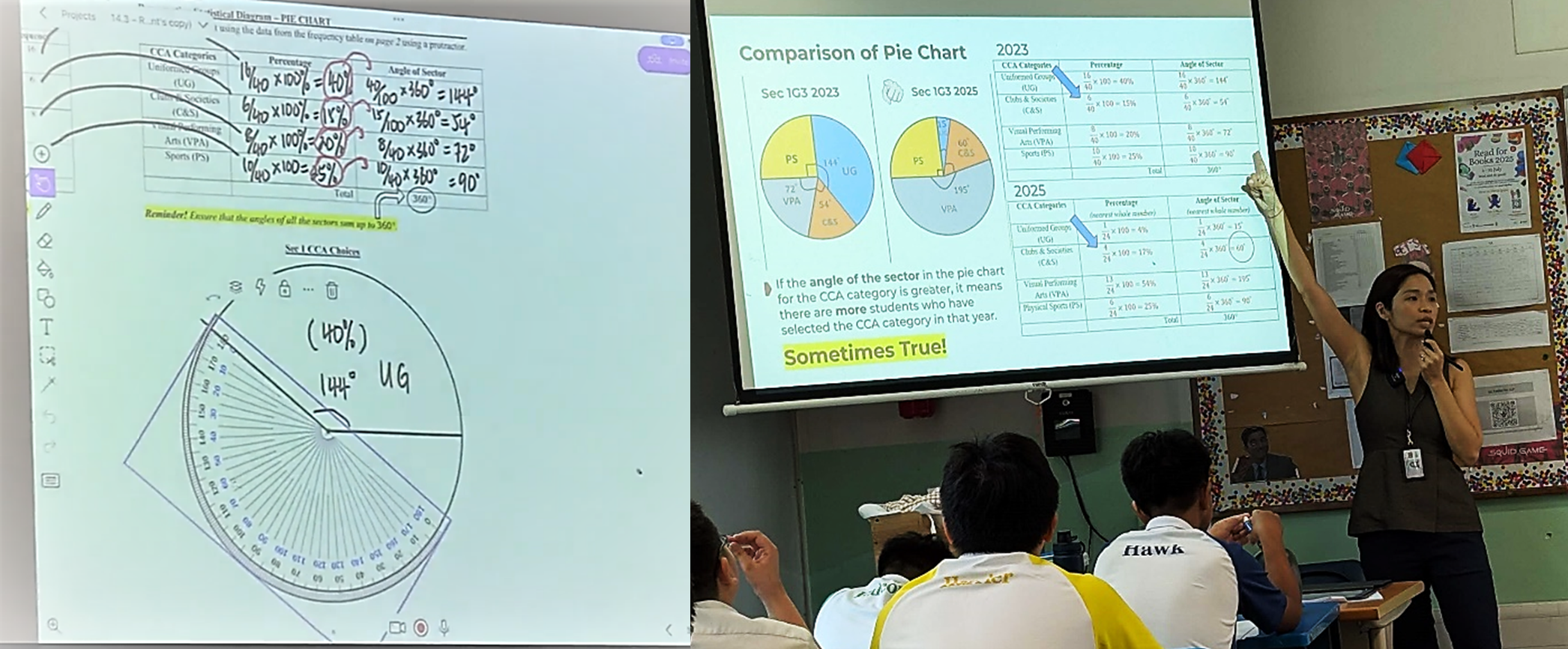
Yaling's statistics lesson at Changkat Changi Secondary School exemplifies effective blended learning, combining pre-lesson SLS activities on pictograms and bar graphs with classroom application to pie chart construction using authentic CCA data. The lesson systematically built understanding through structured comparison of statistical representations, progressing from review and analysis to hands-on construction using GeoGebra, while addressing a common misconception that larger pie chart sectors always indicate a larger number by comparing different-sized datasets. Employing questioning techniques inspired by A/P Helen’s workshop on fostering Critical, Adaptive and Inventive Thinking, Yaling used strategic prompts like "Which statistical diagram is easier to draw?" and "Is it sometimes, always or never true that...?" to develop students' critical thinking about data interpretation. The lesson integrated continuous formative assessment through Classkick uploads, real-time feedback, and confidence scale self-assessment, demonstrating how technology tools can enhance mathematical understanding while encouraging students to justify their reasoning rather than simply providing correct answers.

OEIC Insights from Professional Conversation(s) with NIE, CPDD, and AST

A/P Helen found the professional dialogues to be valuable and mutually beneficial. These conversations enabled all participants to compare education systems, discuss current priorities for Mathematics learning and teaching in a rapidly changing world. She expressed appreciation for meeting educators who demonstrate strong commitment to making a difference for the teachers they work with and, ultimately, for students.

OEIC Insights for Mathematics Education

A/P Helen's educational philosophy is deeply rooted in her multifaceted background as a mathematician and mathematics educator. Her approach is founded on a deep belief that everyone has a right to access the power and beauty of mathematics, viewing her role as facilitating students' pathways to familiarity and fluency with key Mathematical concepts. She advocates for a balanced approach where students develop core skills applicable in routine contexts while engaging in genuine problem-solving, emphasising that Mathematics fundamentally involves generalising from specific cases. Central to her philosophy is the belief that students should understand Mathematics conceptually, not merely perform tasks procedurally, requiring both relational and instrumental understanding through carefully designed classroom activities, discussions, and questioning strategies.

A/P Helen acknowledges that teachers may hold different views of Mathematics and student learning but believes that appropriate professional learning can enhance teachers' repertoires by demonstrating new practices, developing new skills, and generating productive reflection. She recognises the practical challenges in ensuring professional learning programmes reach as many teachers as possible to enhance teaching practices that help students see Mathematics as meaningful, useful, and beautiful while building strong conceptual connections.

We are honoured to have collaborated with A/P Helen through the OEIC Programme and we would like to thank her for her generosity in sharing her insights with our local educators.

(All images featured on this website are used with proper authorisation and necessary permissions have been obtained.)